A scalable, high performance genetic programming / algorithms framework
2020-02-08
Fisher-Yates algorithm for sampling
No matter how simple your code may be, there's no substitute for testing it to make sure it's actually doing what you think it is.
2019-06-03
Symbolic regression with Vita
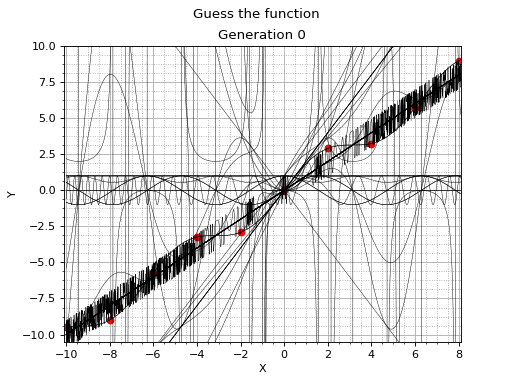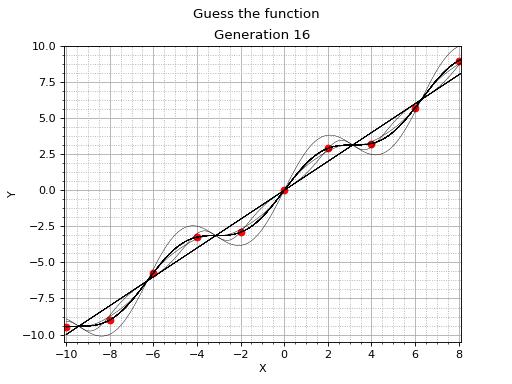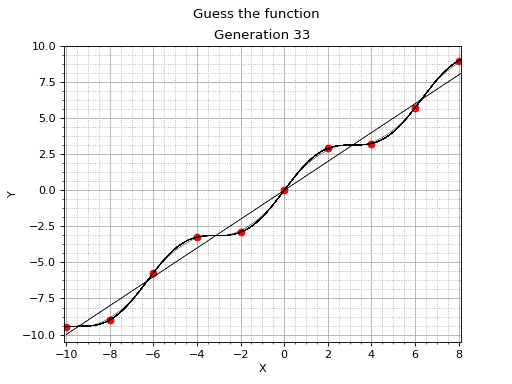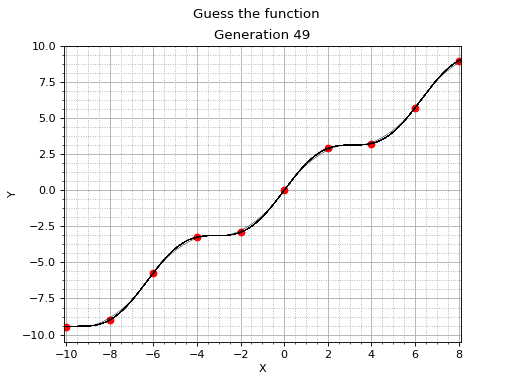
Symbolic regression and genetic programming aren't mainstream machine learning techniques. However, they definitely deserve a considerable amount of attention. This example serves as a gentle and informal introduction to symbolic regression with Vita Genetic Programming Framework.
Read more »
2019-05-16
Mathematical optimization
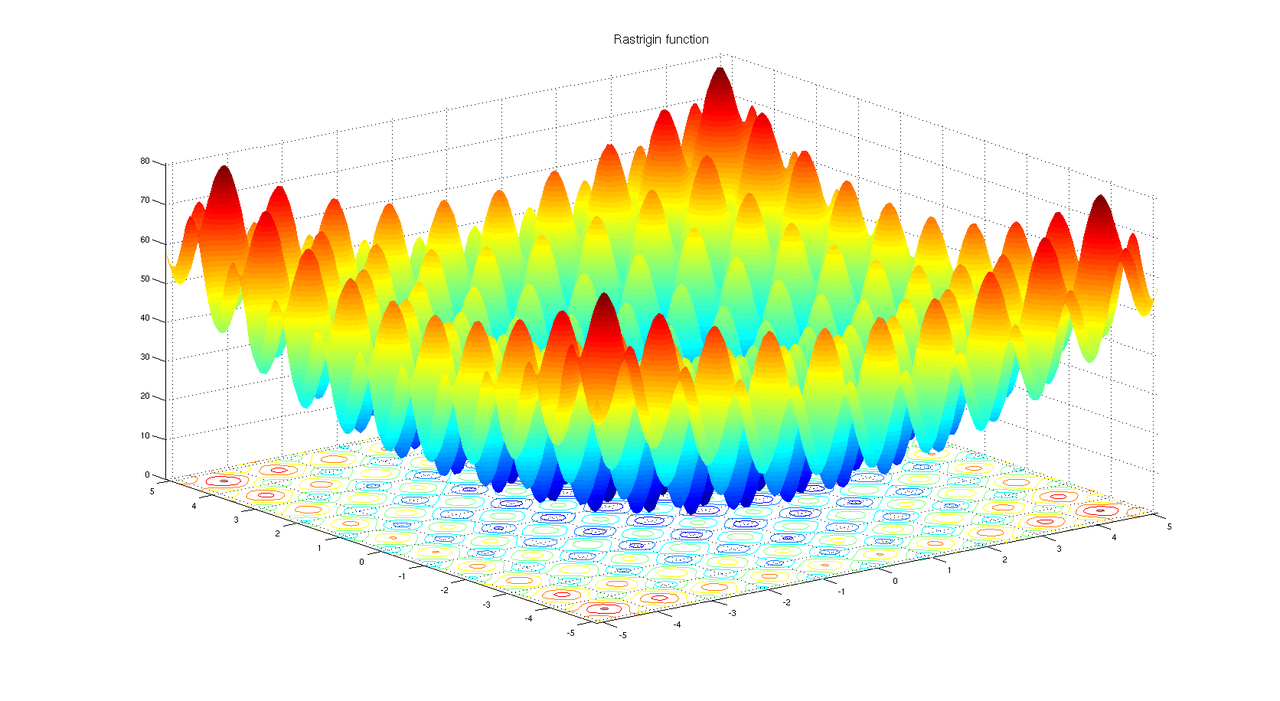
Differential Evolution is an effective, general purpose, black box optimization tool. In this new example we show how to look for the global minimum of the Rastrigin function using Vita and DE.
Read more »
2019-04-06
Completely revised Titanic classification example
The revised example is a step by step guide illustrating the basic elements of classification with genetic programming and the Vita library.
2019-01-19
Slides from C++ Day (Pavia, Italy - 2018)
Slides from the C++Day 2018 (Pavia - Italy) talk are available here: Lessons Learned Developing Evolutionary Algorithms in C++.
The C++ Day is a fall event dedicated to C++ development where professionals, students and companies meet and share experience. The C++ Day has been co-organized with the University of Pavia, in particular with the Physics Department.
The C++ Day is a fall event dedicated to C++ development where professionals, students and companies meet and share experience. The C++ Day has been co-organized with the University of Pavia, in particular with the Physics Department.
2018-08-29
Nonogram puzzle
Nonograms, also known as Japanese puzzles, are logic puzzles that are sold by many news paper vendors. The challenge is to fill a grid with black and white pixels in such a way that a given description for each row and column, indicating the lengths of consecutive segments of black pixels, is adhered to. Although the Nonograms in puzzle books can usually be solved by hand, the general problem of solving Nonograms is NP-hard.
Read more »
2018-01-03
Solving a Tetris-puzzle with GAs
The general challenge posed is to tile a given region with a given set of polyominoes.
TL;DR
GAs aren't the most appropriate tool for this kind of puzzle. GAs tend to produce good but sub-optimal solutions and this behaviour is acceptable only for some combinatorial optimization problems.
Anyway the last example proposed finds a solution almost always (often in a short time) and GAs prove themselves a general, viable path especially when previous knowledge isn't available.
Read more »
Subscribe to:
Posts (Atom)